6.3 阶跃函数

在第 6.2 节中，我们概述了利用拉普拉斯变换解决初值问题的一般步骤。拉普拉斯变换方法的一些最有趣的初等应用出现在具有不连续或脉冲强迫函数的线性微分方程的解中。这种类型的方程经常出现在电流在电路中的流动或机械系统的振动的分析中。在本节和第 6 章的其余部分中，我们将介绍拉普拉斯变换的一些附加属性，这些属性在解决此类问题中非常有用。除非另有明确说明，否则下面出现的所有函数都将被假定为分段连续且具有指数阶，因此它们的拉普拉斯变换存在，至少对于足够大的 $s$。

为了有效地处理具有跳跃不连续性的函数，引入一个称为单位阶跃函数或 Heaviside 函数的函数是非常有帮助的。该函数将用 $u_{c}$ 表示，并定义为

$$u_{c}(t)= \begin{cases}0, & t<c \tag{1}\\ 1, & t \geq c\end{cases}$$

由于拉普拉斯变换涉及区间 $[0, \infty)$ 中的 $t$ 值，因此我们只对 $c$ 的非负值感兴趣。$y=u_{c}(t)$ 的图形如图 6.3.1 所示。我们有点随意地将值 1 赋给了 $t=c$ 处的 $u_{c}$。但是，对于分段连续函数（例如 $u_{c}$），不连续点处的值通常无关紧要。该阶跃也可以是负的。例如，图 6.3.2 显示了 $y=1-u_{c}(t)$ 的图形。

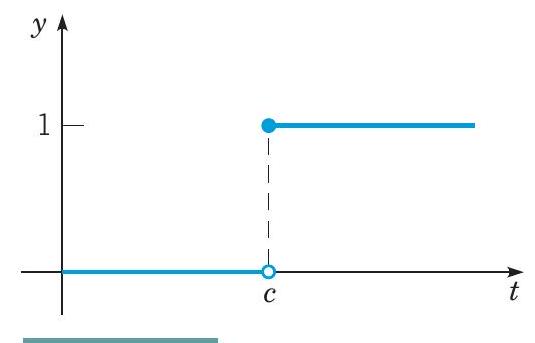
图 6.3.1 $y=u_{c}(t)$ 的图形。

图 6.3.2 $y=1-u_{c}(t)$ 的图形。

如果我们将值 1 与“开”关联，将 0 与“关”关联，那么函数 $u_{c}(t)$ 表示在时间 $c$ 打开的开关。同样，$1-u_{c}(t)$ 表示在时间 $c$ 关闭的开关。

示例 1

绘制 $y=h(t)$ 的图形，其中

$$h(t)=u_{\pi}(t)-u_{2 \pi}(t), \quad t \geq 0 .$$

解：

根据方程 (1) 中 $u_{c}(t)$ 的定义，我们有

$$\begin{aligned} h(t) & =\left\{\begin{array}{ll} 0, & t<\pi, \\ 1, & t \geq \pi \end{array}-\left\{\begin{array}{ll} 0, & t<2 \pi, \\ 1, & t \geq 2 \pi \end{array}= \begin{cases}0-0, & 0 \leq t<\pi, \\ 1-0, & \pi \leq t<2 \pi, \\ 1-1, & 2 \pi \leq t<\infty,\end{cases} \right.\right. \\ & = \begin{cases}0, & 0 \leq t<\pi, \\ 1, & \pi \leq t<2 \pi, \\ 0, & 2 \pi \leq t<\infty .\end{cases} \end{aligned}$$

因此，方程 $y=h(t)$ 具有如图 6.3.3 所示的图形。这个函数可以被认为是一个最初关闭的开关，在 $t=\pi$ 时打开，然后在 $t=2 \pi$ 时关闭；这也通常被称为矩形脉冲。

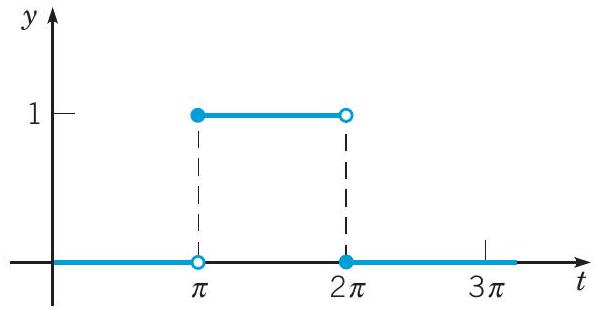
图 6.3.3 $y=u_{\pi}(t)-u_{2 \pi}(t)$ 的图形。

示例 2

考虑函数

$$f(t)=\left\{\begin{align*} 2, & 0 \leq t<4, \tag{2}\\ 5, & 4 \leq t<7, \\ -1, & 7 \leq t<9, \\ 1, & t \geq 9 . \end{align*}\right.$$

绘制 $y=f(t)$ 的图形。用 $u_{c}(t)$ 表示 $f(t)$。

解：

$y=f(t)$ 的图形是分段常数。注意包含每个水平线段的左端点，我们得到图 6.3.4。

图 6.3.4 方程 (2) 中函数的图形。

我们从函数 $f_{1}(t)=2$ 开始，它在 $[0,4)$ 上与 $f(t)$ 一致。为了在 $t=4$ 处产生三个单位的跳跃，我们将 $3 u_{4}(t)$ 加到 $f_{1}(t)$ 上，得到

$$f_{2}(t)=2+3 u_{4}(t),$$

它在 $[0,7)$ 上与 $f(t)$ 一致。$t=7$ 处六个单位的负跳跃对应于加上 $-6 u_{7}(t)$，这给出

$$f_{3}(t)=2+3 u_{4}(t)-6 u_{7}(t)$$

最后，我们必须添加 $2 u_{9}(t)$ 以匹配 $t=9$ 处两个单位的跳跃。因此，我们得到

$$\begin{equation*} f(t)=2+3 u_{4}(t)-6 u_{7}(t)+2 u_{9}(t) . \tag{3} \end{equation*}$$

$u_{c}$ 的拉普拉斯变换，对于 $c \geq 0$，很容易确定：

$$\begin{align*} \mathcal{L}\left\{u_{c}(t)\right\} & =\int_{0}^{\infty} e^{-s t} u_{c}(t) d t=\int_{c}^{\infty} e^{-s t} d t \\ & =\frac{e^{-c s}}{s}, \quad s>0 . \tag{4} \end{align*}$$

注意

$$\mathcal{L}\left\{u_{0}(t)\right\}=\frac{e^{0}}{s}=\frac{1}{s}=\mathcal{L}\{1\}$$

这是因为对于所有 $t \geq 0$，有 $u_{0}(t)=1$。 对于给定的函数 $f$，其定义域为 $t \geq 0$，我们通常希望考虑由下式定义的相关函数 $g$

$$g(t)= \begin{cases}0, & t<c \\ f(t-c), & t \geq c\end{cases}$$

它表示 $f$ 在正 $t$ 方向上平移了距离 $c$，且对于 $t<c$ 时为零；参见图 6.3.5。利用单位阶跃函数，我们可以将 $g(t)$ 写成方便的形式

$$g(t)=u_{c}(t) f(t-c)$$

(a)

(b)

图 6.3.5 给定函数的平移。(a) $y=f(t) ;(b) y=u_{c}(t) f(t-c)$。

单位阶跃函数在拉普拉斯变换的应用中特别重要，因为 $f(t)$ 的变换和其平移 $u_{c}(t) f(t-c)$ 的变换之间存在以下关系。

定理 6.3.1

如果 $f(t)$ 的拉普拉斯变换 $F(s)=\mathcal{L}\{f(t)\}$ 对于 $s>a \geq 0$ 存在，且如果 $c$ 是一个正的常数，那么

$$\begin{equation*} \mathcal{L}\left\{u_{c}(t) f(t-c)\right\}=e^{-c s} \mathcal{L}\{f(t)\}=e^{-c s} F(s), \quad s>a . \tag{5} \end{equation*}$$

反之，如果 $f(t)$ 是 $F(s)$ 的拉普拉斯逆变换，即 $f(t)=\mathcal{L}^{-1}\{F(s)\}$，那么

$$\begin{equation*} u_{c}(t) f(t-c)=\mathcal{L}^{-1}\left\{e^{-c s} F(s)\right\} . \tag{6} \end{equation*}$$

定理 6.3.1 简单地说明了 $f(t)$ 在正 $t$ 方向上平移距离 $c$ 对应于 $F(s)$ 乘以 $e^{-c s}$。为了证明定理 6.3.1，只需计算 $u_{c}(t) f(t-c)$ 的变换：

$$\begin{aligned} \mathcal{L}\left\{u_{c}(t) f(t-c)\right\} & =\int_{0}^{\infty} e^{-s t} u_{c}(t) f(t-c) d t \\ & =\int_{c}^{\infty} e^{-s t} f(t-c) d t \end{aligned}$$

引入新的积分变量 $\sigma=t-c$，我们有

$$\begin{aligned} \mathcal{L}\left\{u_{c}(t) f(t-c)\right\} & =\int_{0}^{\infty} e^{-(\sigma+c) s} f(\sigma) d \sigma=e^{-c s} \int_{0}^{\infty} e^{-s \sigma} f(\sigma) d \sigma \\ & =e^{-c s} F(s) \end{aligned}$$

因此，等式 (5) 成立；等式 (6) 通过对等式 (5) 两边取逆变换得到。

如果取 $f(t)=1$，则出现这个定理的一个简单例子。回忆 $\mathcal{L}\{1\}=1 / s$，我们立即从等式 (5) 得到 $\mathcal{L}\left\{u_{c}(t)\right\}=e^{-c s} / s$。这个结果与等式 (4) 的结果一致。例 3 和例 4 进一步说明了如何在拉普拉斯变换和逆拉普拉斯变换的计算中使用定理 6.3.1。

示例 3

给定函数 $f$ 定义为

$$f(t)= \begin{cases}\sin t, & 0 \leq t<\frac{\pi}{4} \\ \sin t+\cos \left(t-\frac{\pi}{4}\right), & t \geq \frac{\pi}{4}\end{cases}$$

在区间 $0 \leq t \leq 3$ 上绘制 $y=f(t)$ 的图。求 $\mathcal{L}\{f(t)\}$。

解：

$y=f(t)$ 的图形如图 6.3.6 所示。

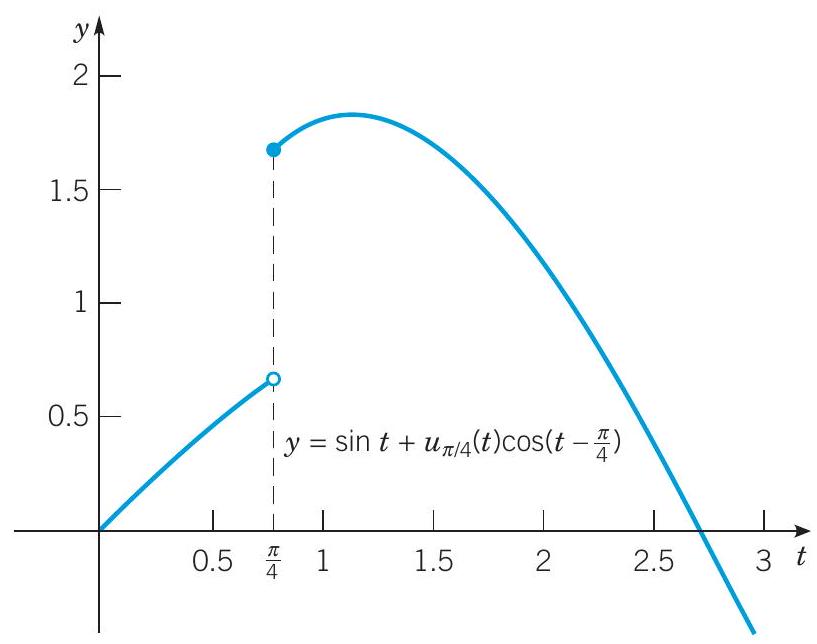
图 6.3.6 例 3 中函数的图形。

注意 $f(t)=\sin t+g(t)$，其中

g(t)=\left\{\begin{array}{ll} 0, & t<\frac{\pi}{4} \\ \cos \left(t-\frac{\pi}{4}\right), & t \geq \frac{\pi}{4} \end{array}

\end{array}=u_{\pi / 4}(t) \cos \left(t-\frac{\pi}{4}\right) .\right.

$$\begin{aligned} \mathcal{L}\{f(t)\} & =\mathcal{L}\{\sin t\}+\mathcal{L}\left\{u_{\pi / 4}(t) \cos \left(t-\frac{\pi}{4}\right)\right\} \\ & =\mathcal{L}\{\sin t\}+e^{-\pi s / 4} \mathcal{L}\{\cos t\} . \end{aligned}$$

$$\mathcal{L}\{f(t)\}=\frac{1}{s^{2}+1}+e^{-\pi s / 4} \frac{s}{s^{2}+1}=\frac{1+s e^{-\pi s / 4}}{s^{2}+1} .$$

您应该将这种方法与直接从拉普拉斯变换定义的非正常积分计算 $\mathcal{L}\{f(t)\}$ 的方法进行比较。

示例 4

求

$$F(s)=\frac{1-e^{-2 s}}{s^{2}}$$

的拉普拉斯逆变换。绘制 $y=f(t)$ 的图。

解：

从逆变换的线性性，我们有

$$\begin{aligned} f(t) & =\mathcal{L}^{-1}\{F(s)\}=\mathcal{L}^{-1}\left\{\frac{1}{s^{2}}\right\}-\mathcal{L}^{-1}\left\{\frac{e^{-2 s}}{s^{2}}\right\} \\ & =t-u_{2}(t)(t-2) \end{aligned}$$

为了方便绘制 $y=f(t)$ 的图形，将该函数写成分段表示形式是有帮助的。这里那意味着

$$f(t)=t-\left\{\begin{array}{ll} 0, & 0 \leq t<2 \\ t-2, & t \geq 2 \end{array}= \begin{cases}t, & 0 \leq t<2 \\ 2, & t \geq 2\end{cases}\right.$$

$y=f(t)$ 的图形如图 6.3.7 所示。

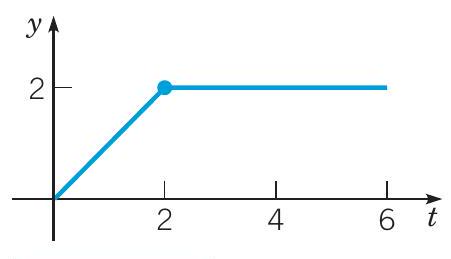
图 6.3.7

以下定理包含拉普拉斯变换的另一个非常有用的性质，该性质在某种程度上类似于定理 6.3.1 中给出的性质。

定理 6.3.2

如果 $F(s)=\mathcal{L}\{f(t)\}$ 对于 $s>a \geq 0$ 存在，且如果 $c$ 是一个常数，那么

”

$$\begin{equation*} \mathcal{L}\left\{e^{c t} f(t)\right\}=F(s-c), \quad s>a+c . \tag{7} \end{equation*}$$

反之，如果 $f(t)=\mathcal{L}^{-1}\{F(s)\}$，那么

$$\begin{equation*} e^{c t} f(t)=\mathcal{L}^{-1}\{F(s-c)\} \tag{8} \end{equation*}$$

根据定理 6.3.2，将 $f(t)$ 乘以 $e^{c t}$ 会导致变换 $F(s)$ 在正 $s$ 方向上平移距离 $c$，反之亦然。为了证明这个定理，我们计算 $\mathcal{L}\left\{e^{c t} f(t)\right\}$。因此

$$\begin{aligned} \mathcal{L}\left\{e^{c t} f(t)\right\} & =\int_{0}^{\infty} e^{-s t} e^{c t} f(t) d t=\int_{0}^{\infty} e^{-(s-c) t} f(t) d t \\ & =F(s-c) \end{aligned}$$

这就是方程 (7)。限制条件 $s>a+c$ 源于观察到，根据定理 6.1.2 的假设 (ii)，$|f(t)| \leq K e^{a t}$；因此 $\left|e^{c t} f(t)\right| \leq K e^{(a+c) t}$。方程 (8) 是通过对方程 (7) 进行逆变换得到的，证明完成。

定理 6.3.2 的主要应用是在计算某些逆变换中，如示例 5 所示。

示例 5

求

$$G(s)=\frac{1}{s^{2}-4 s+5}$$

的逆拉普拉斯变换。

解：

首先，为了避免处理分母 $s^{2}-4 s+5$ 的复数值根，我们在分母中完成平方：

$$G(s)=\frac{1}{(s-2)^{2}+1}=F(s-2),$$

其中 $F(s)=\left(s^{2}+1\right)^{-1}$。由于 $\mathcal{L}^{-1}\{F(s)\}=\sin t$，因此根据定理 6.3.2，

$$g(t)=\mathcal{L}^{-1}\{G(s)\}=e^{2 t} \sin t$$

本节的结果通常在求解微分方程时很有用，特别是那些具有不连续强迫函数的方程。下一节专门讨论说明这一点的示例。